23. 가설검정

1. 가설과 가설검정
   1) 가설이란?
   ${(1)}$ 가설, 특히 통계적 가설이란 모수 또는 분포에 대하여 연구자가 주장하는 내용을 말한다.
   -. 예를 들어서, 홈페이지의 새로운 UI에 대하여 '잠재적 사용자'란 모집단이 존재한다고 가정할 때
   -. 사이트에 실제로 유입된 표본들의 (원본 / 개선안)의 클릭률 차이가 모집단에서도 마찬가지로 유의미할 것이라도 주장할 수 있다. 
   
   2) 가설 검정이란?
   
   ${(1)}$ 연구자가 주장한 가설이 실제로도 유의미한지 참 / 거짓을 판별하는 방법론을 가설검정이라고 한다.
   
   ${(2)}$ 가설 검정엔 귀무가설과 대립가설이라는 두 개념이 등장한다.
   -. 대립가설 : 연구가설이라고도 표현한다. 연구자가 관심을 갖고 있는(즉 연구자가 주창한) 가설을 의미한다.
   -. 귀무가설 : 영가설이라도고 표현한다. 대립가설에 대비되는 개념으로, 연구자는 귀무가설을 기각함으로서 마침내 대립가설이 참임을 증명할 수 있다.
   
   -. 엄밀한 정의로는 아래와 같이 표현할 수 있다.

   확률변수 X가 pdf $f(x;\theta)$를 가진다고 하자. 이 때 $[X_{1}, ..., X_{n}]$은 X에서 추출한 확률표본이라 하자. 모수 $\theta$가 모수공간 $\Omega$에 속할 때,  $\Omega$를 두 부분공간 $\omega_{0}$, $\omega_{1}$로 쪼갤 수 있다고 하자. (두 공간에 겹치는 부분은 존재하지 않는다.) 이 때, 가설 검정이란 다음의 가설을 검정한다. $H_{0}$(귀무가설) : $H_{0} \in \omega_{0}$ $H_{1}$(대립가설) : $H_{1} \in \omega_{1}$  한편, 가설검정은 실제로는 확률표본 $[X_{1}, ..., X_{n}]$에 의거해 수행하며, 이 때 확률표본의 전체 공간을 D라고 하고, D에 일부분을 점유하는 부분공간을 C라고 가정하자. 확률표본을 이용한 가설검정에 대한 정의는 다음과 같다. $H_{0}(귀무가설) : [X_{1}, ..., X_{n}] \in C$ $H_{1}(대립가설) : [X_{1}, ..., X_{n}] \in C^{c}$ 즉, 확률표본(혹은 그의 함수)이 부분공간 C에 속하면 귀무가설을 채택하고, C 여집합에 속하면 대립가설을 채택한다. 이 때, C를 기각역이라고 표현한다.

2. 가설검정의 오류
   1) 가설검정엔 오류의 종류에 따라 1종오류와 2종오류로 분류할 수 있다.
   
   ${(1)}$ $[X_{1}, ..., X_{n}] \in C$ 라서 $H_{0}$를 기각했으나(즉, $H_{1}$을 채택했으나), 사실 $\theta \in w_{0}$ 였다면 이를 1종 오류라고 한다.
   
   ${(2)}$ $[X_{1}, ..., X_{n}] \in C^{c}$ 라서 $H_{0}$를 유지했으나(즉, $H_{1}$을 채택하지 못했으나), 사실 $\theta \in w_{1}$ 였다면 이를 2종 오류라고 한다.

   	$H_{0}$가 참	$H_{0}$가 거짓
   $H_{0}$ 기각함	1종 오류	옳은 결정
   $H_{0}$ 채택함	옳은 결정	2종 오류

3. 유의수준, 검정력과 검정력함수
   1) 유의수준 $\alpha$
   ${(1)}$ 우선, 유의수준 $\alpha$에 대해 먼저 엄밀하게 정의하고 넘어가면 다음과 같다.

   모수 $\theta \in w_{0}$일 때, 기각역 C가 설정되었다고 한다면  $\max_{\theta \in w_{0}} P[(X_{1}, ..., X_{n}) \in C]$를 유의수준 $\alpha$라고 지칭한다.

   
   -. 그림자료와 함께 $\alpha$의 의미에 대해 좀 더 자세하게 설명하면
   

   이 함수는 유의수준(크기) $\alpha$로부터 정의역에 대한 구간인 기각역 C를 역으로 구하는 역연산이라고 생각해야한다. 즉, 우리는 기각역에 속하는 어떤 값(=임계값)을 기준으로 가설검정을 수행하고 싶어할 때 값을 결정하는데 필요한 근거 자료 중 하나는 1종 오류를 범할 확률이며 연구자는 이 자료를 토대로   귀무가설($H_{0} : \theta \in w_{0}$)가 참일 때 이를 기각할 때의 리스크( = 1종 오류)를 최소화 해야한다. 연구자가 $\alpha = 0.05$ 등으로 이 리스크를 결정할 때, 기각역 C도 동시에 결정되며 기각역 C에 속하는 임계값도 결정이 가능하다.

   2) 검정력
   ${(1)}$ 유의수준 $\alpha$를 만족하는 기각역을 설정하는 방법은 그야말로 무한개의 경우의수가 발생한다.
   
   -. 가령, 귀무가설을 참이라고 가정할 수 있는 기각역은 기각역을 아예 설정하지 않는 것($C = \phi$)에서부터 표본공간 D를 전부 점유하는($C = D$)까지 설정이 가능하다.
   
   ${(2)}$ 극단적으로, 기각역을 아예 설정하지 않은 경우($C = \phi$)를 가정했을 때
   -. 이 가설검정은 항상 1종 오류가 0일 것이며($H_{0}$를 절대 기각하지 않기 때문이다),
   -. 반대로 2종오류는 항상 1일 것이다($H_{0}$를 항상 채택하기 때문에, $H_{0}$가 거짓인 경우 그 확률은 항상 1이 된다.)
   
   ${(2)}$ 좋은 가설검정이란, 이렇듯 서로 Trade-off 관계에 있는 1종오류와 2종 오류 사이에서 적절한 균형을 잡아 1종오류($=\alpha$)를 최소화 하면서도 2종 오류를 최소화 하는 기각역을 설정하는 것이다. 
   
   -. 이 때, 1종오류의 확률을 유의수준 $\alpha$로 놓고, 2종오류의 확률을 $\beta$라고 하자.
   
   -. 이 때, 좋은 가설검정이란 2종오류의 확률 $\beta$를 최소화 하는것이며, 이는 다시 말하면 $\theta \in \omega_{1}$의 확률을 최대화하는 크기 $1-\beta$를 도출하는 것이다.
   
   ${(3)}$ 여기서 검정력이란 개념이 도출된다. 검정력 개념의 엄밀한 정의는 다음과 같다.

   모수 $\theta \in \omega_{1}$ 에 대하여 $1 - \beta = 1 - p_{\theta}[2종오류] = p_{\theta}[(X_{1}, ..., X_{n})] \in C]$ 를 검정력이라고 정의한다.

   -. 다시 말해, 검정력이란 연구가설($H_{1}$) 에 속하는 분포가 참이라고 가정했을 경우, 기각역 C에 속해있는 확률을 의미한다.
   
   

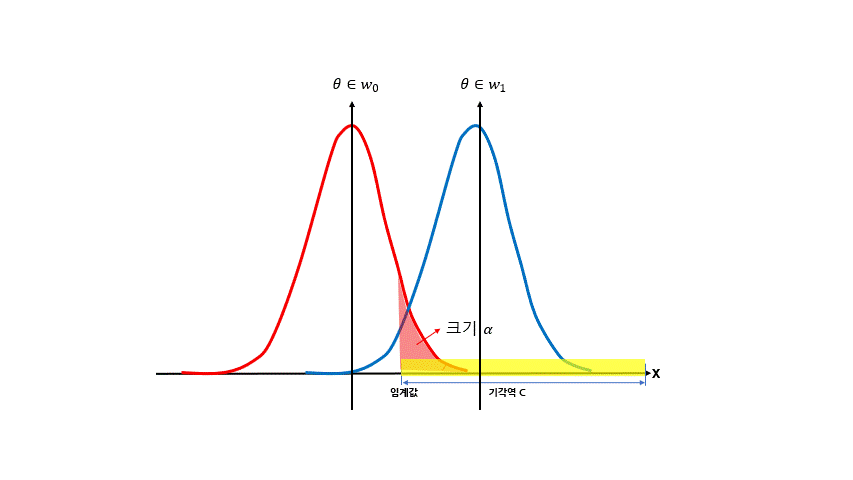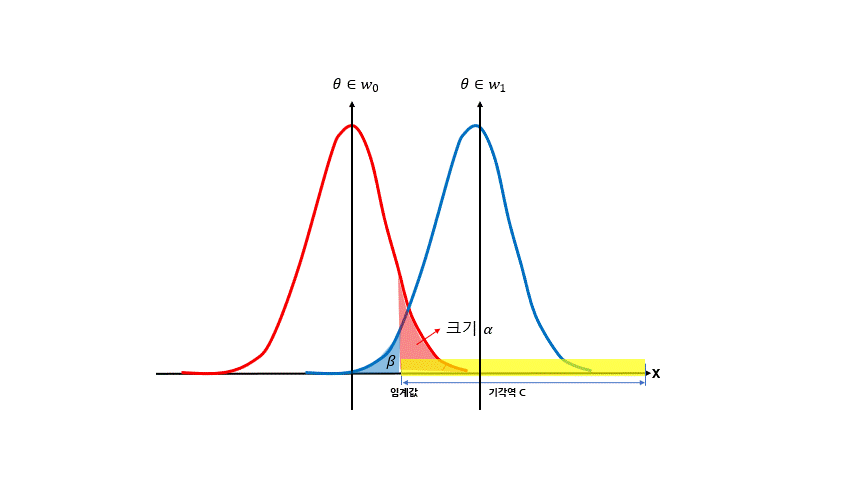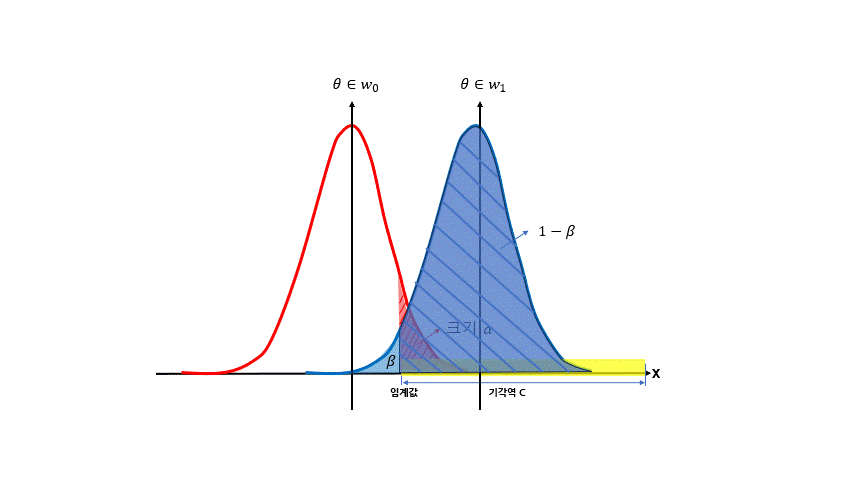
   좋은 가설검정이란, 기각역 C로부터 임계값을 도출했을 때, 그 임계점이 $\alpha$와 $\beta$를 모두 최소화하는 지점이어야 한다. $\theta \in w_{0}$ 일때 유의수준 $\alpha$인 기각역 C는 매우, 무수히 많으나  여기에 더해 $1 - \beta$ = 검정력을 최대화(Maximization)한다는 조건이 붙은경우 그 기각역 C를 결정하는 경우의수는 확 줄어들게 된다. 그 지점이 바로 좋은 가설검정을 하는 임계값의 지점이다.

   3) 검정력 함수
   ${(1)}$ 이 때, 다음을 검정력을 계산하는 검정력함수라고 표현한다.
   $$P_{\theta \in \omega_{1}} = [(X_{1}, ... , X_{n}) \in C]$$
   
   
4. 가설 검정의 방법
   1) 유의수준 $\alpha$, 검정력 $1 - \beta$으로부터 최선의 기각역과 그에 따른 임계값을 도출했다고 가정하자
   
   2) 이제, $[(X_{1}, ..., X_{n}]$를 이용하여 어떤 통계량, 즉 검정통계량 
   $$T = [(X_{1}, ..., X_{n}]$$ 를 계산할 수 있다.
   
   3) 이제, 우리가 계산한 검정통계량 T에 대하여 다음의 경우의 수를 상정할 수 있다. 이것을 가설 검정이라고 한다.
   

   귀무가설이 참인 경우	$$T([X_{1}, ..., X_{n}]) \in C$$
   대립가설이 참인 경우	$$T([X_{1}, ..., X_{n}]) \in C^{c}$$

   
   4) 혹은, 정의역 차원에서의 기각역(혹은 임계값)이 아닌 확률 자체를 이용하여 가설검정을 수행할 수 있다.

   귀무가설이 참인 경우	유의수준 $\alpha$에 대하여 $P_{\theta \in \omega_{0}}[(T([X_{1}, ..., X_{n}]) \in C] \geq \alpha$
   대립가설이 참인 경우	유의수준 $\alpha$에 대하여 $P_{\theta \in \omega_{0}}[(T([X_{1}, ..., X_{n}]) \in C] < \alpha$

   
   
   

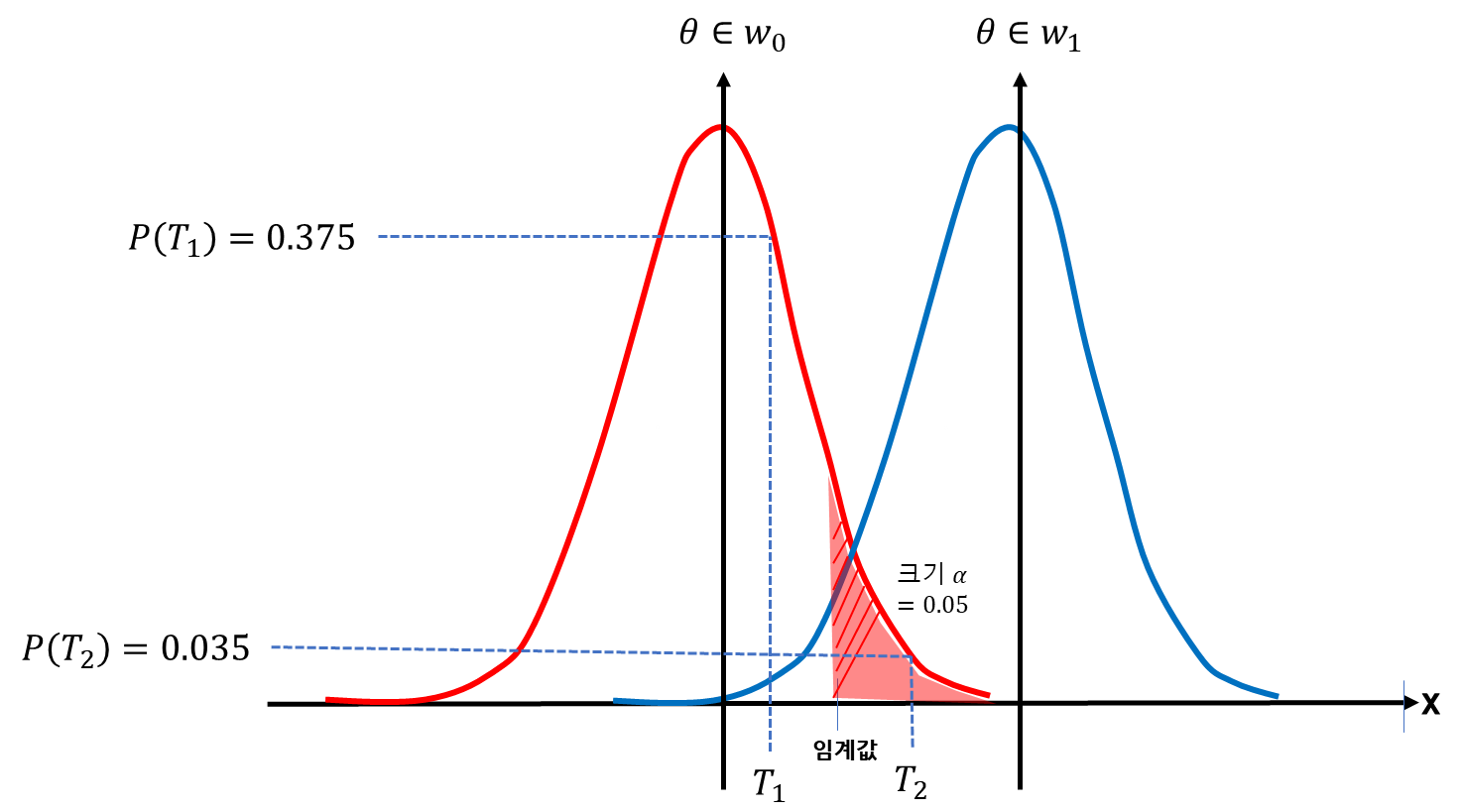
   가설 검정의 예시는 다음과 같다. 각각의 통계량 $T_{1}$과 $T_{2}$가 있다고 가정하자. 우리의 가설은 다음과 같다. $T_{1}$에 대하여 $$H_{0} :  T_{1} = \omega_{0} \ vs \ H_{1} :  T_{1} > \omega_{0}$$ $T_{2}$에 대하여 $$H_{0} :  T_{2} = \omega_{0} \ vs \ H_{1} :  T_{2} > \omega_{0}$$ ①검정통계량, 혹은 ②검정통계량의 확률을 이용하는 양쪽 방법으로 모두 검증했을때, 우리는 다음과 같은 결론을 내릴 수 있다. -. $T_{1}$에 대하여, $T_{1}$은 기각역에 속하지 않고, $P(T_{1}) > \alpha = 0.05$ 이므로, 우리는 귀무가설 $H_{0}$를 기각할 수 없다. -. $T_{2}$에 대하여, $T_{2}$은 기각역에 속해 있고, $P(T_{1}) < \alpha = 0.05$ 이므로, 우리는 귀무가설 $H_{0}$를 기각하고 대립가설 $H_{1}$을 채택한다.