25. 몬테카를로 방법

<수정사항>

2024-12-16 채택-기각 알고리즘에 대한 내용 대거 보강

1.  몬테카를로 방법
   
   1) 특정한 분포나 표본(Sample)로부터 역으로 관측값을 생성하는 방법론
   ${(1)}$ 반복된 무작위 추출을 이용하여 문제를 푸는 목적이 되는 확률분포를 근사적으로 모델링한다.
   -. 즉, 무작위 추출된 표본값을 근사적으로 모델링된 분포를 거쳐 변환한 시뮬레이션 실현값은 우리가 알길 원하는 확률분포의 실현값으로 간주해도 무방하다
   -.몬테카를로 방법을 통해, 실질적으로 닫힌 형태로 분포를 구할 수 없는 현실의 많은 문제를 시뮬레이션을 통해 대리 확인할 수 있다는 점에서 장점을 가진다.
   -. 그러나, 수많은 무작위 반복 실험을 거쳐야하기 때문에 뛰어난 컴퓨팅파워가 없는 경우 실험이 어려운 경우가 많다.
   
   ${(2)}$ 구체적으로는 다음의 단계를 따른다.
   -. 균등분포에서 무작위 표본값 U를 추출
   -. 추출한 무작위 표본값을 (확률변수 X의 CDF F의) 역함수 $F^{-1}(Y)$를 통해 변환
   -. 변환된 값은 우리가 원하는 확률변수 X CDF F를 근사하기 때문에, 이 실현값은 해당 분포에서 추출되었다고 간주해도 무방

   확률변수 U가 균등분포 U(0,1)을 따른다고 하자. F가 임의의 연속형 확률변수라고 하자. 이때, 확률변수 $X = F^{-1}(U)$는 분포함수 F에서 추출한 확률분포의 실현값이다.

   
   2) 채택 - 기각 알고리즘
   
   ${(1)}$ 그러나, 확률변수X 의 CDF를 닫힌 형태로 구하는것은 대부분 어렵기 때문에, 그 역함수를 구하는것도 대부분의 경우 매우 쉽지 않다.
   따라서, 그 대처법이 필요한데, 닫힌 형태가 잘 알려져있거나 그 역함수의 값을 알고리즘적 방법으로 구하기 쉬운 대리 확률분포의 CDF G를 도입(실질적으로는 pdf g)함으로서 해결한다. 
   
   이를 채택 - 기각 알고리즘(Acceptance-rejection Method)이라고 한다.
   
   -. 균등 분포에서 무작위 표본값 U 추출
   -. 상대적으로 역함수를 구하기 쉬운 PDF를 가진 대체 확률분포의 pdf g를 도입
   -. g의 역함수 $g^{-1}(U)$를 이용하여 X의 역 Y를 계산
   -. 다음의 기준에 따라 채택 / 기각을 결정
   

   $U \leq \frac{f(Y)}{cg(Y)}$ True면 Y를 추출값에 포함하고, False면 Y를 폐기하고 다음 iteration 진행

   -. 다시 말해, 균등분포의 무작위 표본값 U를 이용하여 Y를 X의 확률분포에서서 추출한 값으로 채택(Accpetance)하거나, 혹은 기각(Rejection) 하는 알고리즘이다. 
   
   ${(2)}$  다음의 증명을 통해 이 방법론이 사실임을 증명할 수 있다.

   CDF의 역함수 $F^{-1}$를 생각해보자 $P(F^{-1}(X) | X \leq x)$ 에 대해서, 이를 Y로 변환하여 정리하면 다음과 같이 정리할 수 있다 $F(y) = P(Y | Y \leq y)$ 이제 우리는 $P(Y \leq y | U \leq \frac{f(Y)}{cg(Y)})$가 $F(y)$와 동등함을 보일 것이다

   우선, 베이즈 정리에 대해 짚고 넘아가자. 베이즈 정리를 이용하면 다음은 참이다 $P(A|B) = P(B|A) * \frac{P(A)}{P(B)}$ $A = \{Y \leq y\}$, $B = \{U \leq \frac{f(Y)}{cg(Y)}\}$라고 하자 ..... ①  $P(A|B) = P(Y \leq y | U \leq \frac{f(Y)}{cg(Y)})$ 를 베이즈 정리를 이용해 알기 위해서는  $P(B|A)$와 $P(B)$에 대해서 알아야 한다

   <$P(B|A)$ 구하기> $P(U \leq \frac{f(Y)}{cg(Y)} | Y \leq y)$ 이 때, $G(y) = P(G(Y) | Y \leq y)$일 때, 조건부 분포의 정의에 따라 다음과 같은 형태로 변환할 수 있다. $\frac{P(U \leq \frac{f(Y)}{cg(Y)} , Y \leq y)}{G(y)}$ 조건부 분포의 정의에 따라 $\int_{a}^{b}f(A,B)dY = \int_{a}^{b}f(A|B)\cdot f(B)dY$가 성립하므로, ①을 이용하고 동시에 $Y=w$로 치환하면 $\int_{-\infty}^{y}\frac{P(U \leq \frac{f(Y)}{cg(Y)} | Y = w\leq y)}{G(y)}g(w)dw$ 이 때, $P(U \leq \frac{f(Y)}{cg(Y)})$는 균등분포의 cdf를 구하는것과 같고, U는 (0,1) 사이의 균등 분포이므로 $P(U \leq \frac{f(Y)}{cg(Y)}) = \frac{f(Y=w)}{cg(Y=w)}$ 다시 정리하면 $=\frac{1}{G(y)}\int_{-\infty}^{y}\frac{f(w)}{cg(w)}g(w)dw$ $= \frac{1}{G(y)}\int_{-\infty}^{y}f(w)dw$ $=\frac{F(y)}{cG(y)}$ ...... ②

   <$P(B)$ 구하기> $P(B)$를 구하는 것은 간단하다.  $P(B) = \int_{-\infty}^{\infty}\frac{f(y)}{cg(y)} \cdot g(y)dy$ $= \frac{1}{c} \int_{\infty}^{\infty}f(y)dy$ $= \frac{1}{c}$ ....... ③

   <다시 베이즈 정리로> $P(A|B) = P(B|A) * \frac{P(A)}{P(B)}$를 구한 값을 이용해 다시 정리하면 $\frac{F(y)}{cG(y)} \cdot \frac{G(y)}{1/c} = F(y)$ 다시 말해, $U \leq \frac{f(Y)}{cg(Y)}$를 이용하여 $P(Y \leq y |\leq \frac{f(Y)}{cg(Y)})$를 구하는것은 CDF $F(y)$를 구하는것과 동등하며, 이제 채택-기각 알고리즘을 사용하는 이유는 정당화 되었다.

2. 몬테카를로 방법의 예시
   1) 몬테카를로 방법을 활용한 가설 검정

   X가 평균 $\mu$를 따르는 (임의의)확률변수라 하자. X의 pdf는 알려져있다고 하자. 다음의 귀무가설과 대립가설을 검정하고자 한다. $H_{0} : \mu = 0$ vs $H_{1} : \mu > 0$ 이 때, 이 검정을 분포 X에서 추출한 n=20인 표본에 근거한 다음의 통계량을 기반으로 수행할 수 있다. $$\overline{x} = \sum\frac{X_{i}}{n}$$ $$S^{2} = \frac{\sum{(X_{i} - \mu)^{2}}}{n-1}$$ 라고 정의할때, 다음의 검정통계량 $$t = \frac{\overline{x}}{s/\sqrt{20}}$$ 가 $\alpha = 0.05$, $df = 19$인 t분포를 따를때 그 임계값 t = 1.729보다 크면 $H_{0}$를 기각 (여기까지는 몬테카를로 시뮬레이션이 개입하지 않는다.)

   한편, 우리는 다음의 문제에 관심을 가질수 있다. 우리는 유의수준 $\alpha$를 0.05로 가정하였다. 하지만, 임의의 확률변수 X의 분포에서 유의수준 $\alpha$가 진짜로 0.05인지, 아니면 X 자체가 여러 분포의 혼합으로 오염되어서 $\alpha$가 그보다 더 큰 값을 갖는지는  다음의 몬테카를로 시뮬레이션을 통해 생성한 t분포의 실현값들을 통해 간접적으로 확인해볼 수 있다.

   단계	절차
   1	k = 1, I = 0으로 초기화한다. 반복 횟수 N를 정의한다.
   2	X로부터 크기 20인 확률표본을 생성한다.
   3	이 확률표본들을 이용하여 검정통계량 t를 위의 산식에 따라 계산한다.
   4	만약 t > 1.729이면, I를 1 증가시킨다. t > 1.729 여부와 상관없이 k는 무조건 1씩 증가한다.
   5	만약 k가 반복횟수 N에 도달하면 반복을 종료한다.
   6	반복 종료 후, $\widehat{\alpha} = \frac{I}{N}$을 계산한다. 이 때, 구한 $\widehat{\alpha}$에 대한 신뢰구간은 다음과 같이 구한다 $$\alpha \in (\widehat{\alpha} - 1.96(\sqrt{\widehat{\alpha}(1-\widehat{\alpha})/N}), \quad \widehat{\alpha} - 1.96(\sqrt{\widehat{\alpha}(1-\widehat{\alpha})/N}))$$ 이 때, 1.96이란 상수는 비율 $\widehat{\alpha} = \frac{I}{N}$에 대한 중심극한정리를 활용하였다.  이 때, 만약 $\alpha = 0.05$라는 가설이 참이라면, 이 신뢰구간 내에 포함되어 있을것이다.

   
   2) 지수분포의 몬테카를로 방법 
   

   ${(1)}$ 지수분포의 pdf는 아래와 같다. $$F(x) = 1 - e^{-\lambda x}$$ ${(2)}$ 균등분포를 따르는 확률변수 U에 대하여 pdf의 역함수는 다음과 같이 정의할 수 있다. $$F^{-1}(U) = -(\frac{1}{\lambda}) log(1-u)$$ ${(3)}$ 이제 남은것은, 균등분포에서 임의의 값을 추출하여 이 역함수의 실현값을 구하는 것이다.

   
   3) 몬테카를로 적분
   ${(1)}$ 몬테카를로 적분의 유도
   -. 어떤 함수 $g(x)$의 역도함수가 닫힌형태로 표현되지 않을 경우엔 수치적분으로 이를 구해야 한다.
   -. 이 때, 수치적분의 방법 중 하나로 몬테카를로 방법론을 이용한 적분을 이용할 수 있고, 이는 아래와 같이 유도 가능하다.
   

   $\int_{a}^{b}g(x)dx$ 라는 적분식을 정의하자.  만약, 여기서 X를 확률변수라 가정하고, 확률변수 X가 균등분포 U(a,b)를 따른다고 하자. 균등분포의 pdf는 $\frac{1}{b-a}$이다. 균등분포의 pdf를 적분식 내부에 갖도록 적분식을 변형하면  ${(1)}$ $\int_{a}^{b}g(x)dx = (b-a)\int_{a}^{b}g(x)\frac{1}{b-a}dx$ 이다. 한편, 적분식 부분을 보면, 이는 g(x)라는 값에 대하여 기댓값을 구하는 공식이란걸 알 수 있다. 다시 말해  $(b-a)E[g(x)]$와 같다. 이제, 확률변수 X로부터 표본 $[X_{1}, ... X_{n}]$을 추출하고, 이를 이용하여 다음의 통계량을 가정하자 $$Y_{i} = (b-a)E[g(x_{i})]$$ 이 때, $[Y_{1}, ..., Y_{n}]$는 어떤 확률변수 Y에서 추출한 확률표본이라고 하자. 이 확률표본들의 평균 $$\overline{Y} = \sum \frac{y_{i}}{n}$$ 을 정의하자.

   평균이 어떤 값에 대한 불편추정량인지 알아보자. $$E(\overline{Y}) = \frac{1}{n} \sum_{i=1}^{n} (b-a)E[g(x_{i})] = \frac{b-a}{n} E[\sum_{i=1}^{n}g(x_{i})]$$ 한편, $E[\sum_{i=1}^{n}g(x_{i})] = E[g(x_{1}) + \dots + g(x_{n})]$ 인데, 확률표본 $[X_{1}, \dots , X_{n}]$ 의 기댓값은 추출의 근본인 확률변수의 기댓값을 구하는것과 동일하다. 다시 말해 $$E[\sum_{i=1}^{n}g(x_{i})] = E[g(x) + \dots + g(x)] = n E[g(x)]$$ 이다.  도출된 항들을 모두 모아 다시 정리하면  $$\frac{b-a}{n} \cdot n E[g(x)] = (b-a)E[g(x)] = (b-a)\int_{a}^{b}g(x)\frac{1}{b-a}dx = \int_{a}^{b}g(x)dx$$ 이다. 따라서 $\sum \frac{Y_{i}}{n}$ 은 $\int_{a}^{b}g(x)dx$의 불편추정량이 되고, 적분식에 대한 추정을 원했던 우리의 의도를 달성할 수 있다.

   
   ${(2)}$ 몬테카를로 적분의 예시 : 몬테카를로 적분을 이용한 $\pi$값의 추정

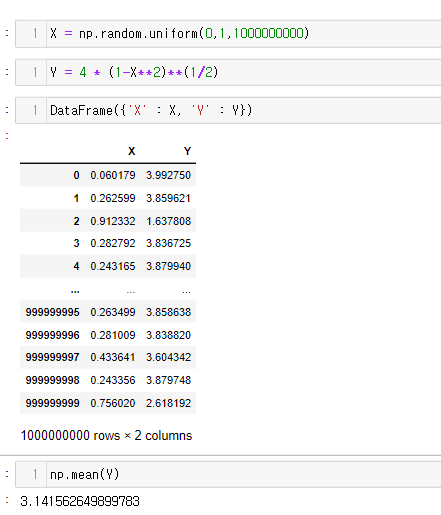
   $\int_{a}^{b} \frac{1}{\sqrt{1-x^{2}}}dx = arctan(x)$ 한편, $arctan(1) = \frac{\pi}{4}$ 이므로, $4 arctan = \int_{a}^{b} \frac{4}{\sqrt{1-x^{2}}}dx = \pi$ 즉, $g(x) = \frac{4}{\sqrt{1-x^{2}}}$ 로 정의할 수 있다.  한편, 균등분포 (0,1)에서 확률표본 $[X_{1}, ..., X_{n}]$을 뽑고,  $Y_{i} = \frac{4}{\sqrt{1-x_{i}^{2}}}$를 정의하여 변환된 값을 구한다. 그 평균 $\overline{Y}$는 이 적분의 불편추정량이므로 이를 구하면  $\pi$의 값 3.141592....에 근사한 값이 도출된다 . $4 * (1 - x ^{2})^{1/2}$에 대한 몬테카를로 적분 결과. 파이썬의 Numpy를 이용하여 1000억개의 균등분포 표본값을 생성하였고 이를 $4 * (1 - x ^{2})^{1/2}$를 이용하여 변환한 Y값의 평균을 구하면 $\pi$와 거의 유사한 3.141562...가 나오게 된다.