Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
Tags
- 프로그래머를 위한 선형대수 #선형대수 #행렬계산
- 프로그래머를 위한 선형대수 #선형대수 #LU분해
- 프로그래머를 위한 선형대수 #선형대수 #고유분해 #고윳값 #고유벡터
- Media Mix Modeling
- Marketing Mix Modeling
- 미적분 #평균값 정리 #로피탈의 정리 #접선의 방정식
- 프로그래머를 위한 선형대수 #선형대수 #고유값 #고유벡터 #고유분해
- Optimization
- bayesian
- 미적분 #접선의 방정식 #최적화 #뉴턴법 #뉴턴-랩슨법
- mmm
- 프로그래머를 위한 선형대수 #선형대수 #고유값 #고유벡터 #야코비 회전법 #QR법 #하우스홀더반사 #행렬회전
- 미적분 #사인과 코사인의 도함수
- lightweightmmm
- 수리통계
- bayesian inference
- 미적분
- 시계열분석 #Time-Series Analysis #이상탐지 #Anomaly Detection #Spectral Residual #CNN #SR-CNN
Archives
- Today
- Total
문과생 네버랜드의 데이터 창고
8. 뉴턴법 본문
- 정의
1) f(x) = 0에 도달하는 수렴 방식의 수렴방식의 반복법
2) 반복법 자체의 방법론은 아래와 같은 예시를 따른다.
${(1)}$ $F(X_{n}) = X_{n + 1}$의 무한 수열
${(2)}$ 예를 들어, $cos(x_{0})$를 세 번 반복하면
${(3)}$ $cos(cos(cos(x_{0})))$이 된다. 즉 계산기의 cos 버튼을 세 번 누르는것과 같다.
${(4)}$ 이 경우, $cos(0.7391)$에서 자기 자신과 같은 0.7391이 나오는데 이 지점이 바로 고정점이다.
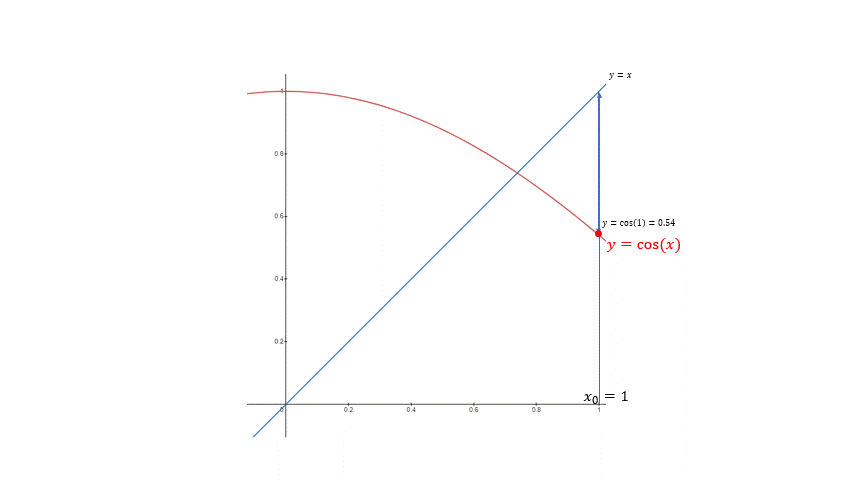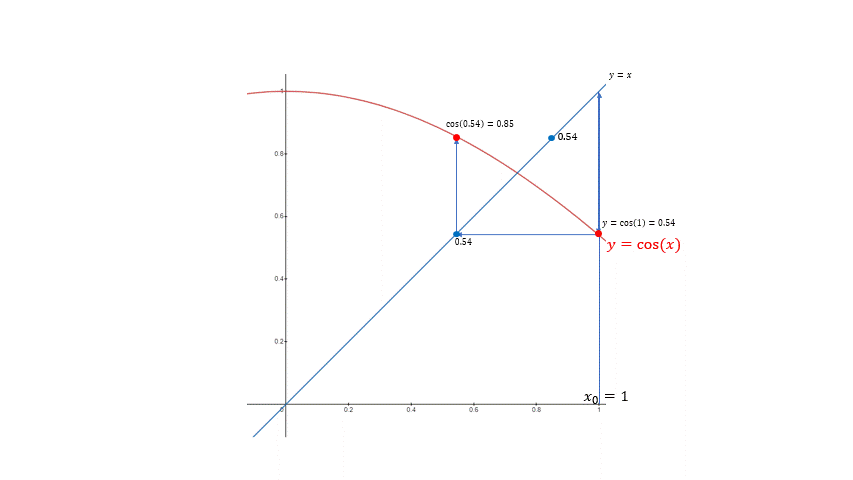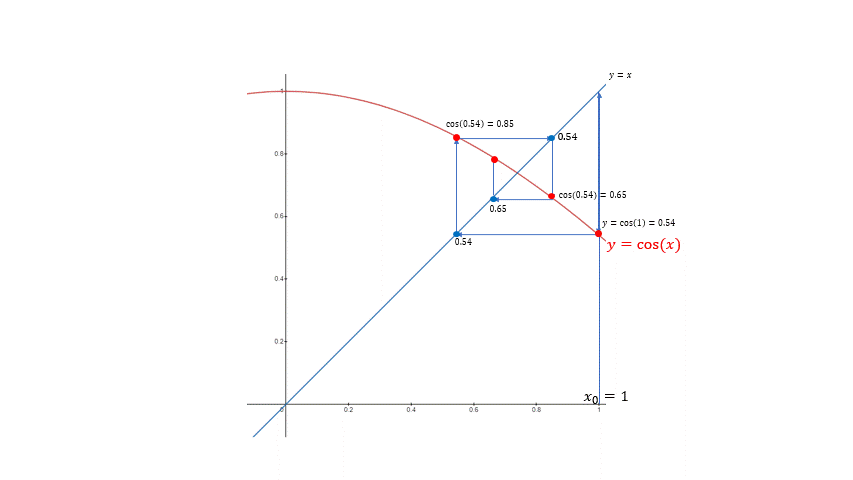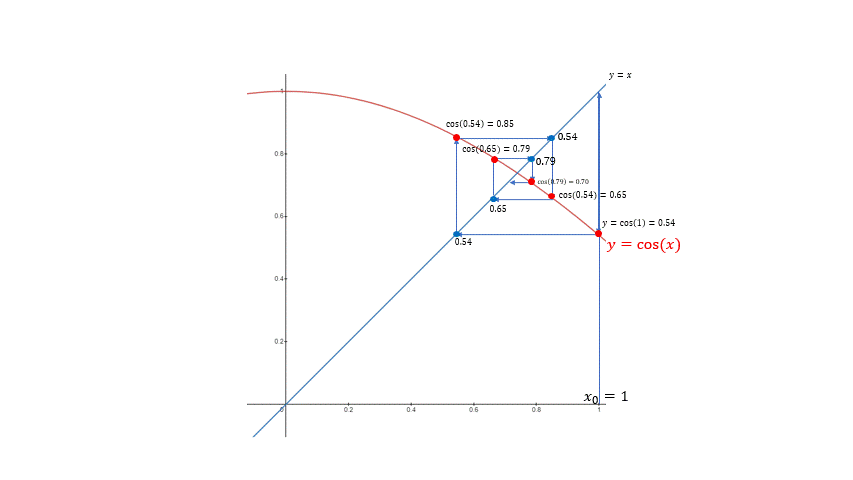
반복법 $F(X_{n}) = X_{n + 1}$의 예시. 점차적으로 고정점 0.7391에 가깝게 다가가게 된다.
${(5)}$ 이 때, 총 이동 길이는 그 기울기인 $\frac{F(x)}{\partial x}$를 따르는데, 따라서 $F'(x) < 1$이면 이 함수는 결국 특정값으로 수렴하고, $F'(x) \geq 1$ 이면 발산한다.
3) 뉴턴법은 반복법을 확장하여 다음의 문제를 푼다
${(1)}$ $X_{n+1} = F(x_{n}) = X_{n} - c \cdot f(x_{n})$
${(2)}$ 이 때, 적절한 c를 고르면 이 문제를 해결할 수 있게 된다.
${(3)}$ 함수를 고정점으로 수렴하게 하는 $x^{n}$의 해 $x^{*}$가 존재한다고 가정하면
-. $\displaystyle \lim_{x \to x^{*}}x_{n}-c \cdot f(x_{n})=x^{*}-cf(x^{*})=x^{*}=F(x^{*})$
-. $x^{*}-cf(x^{*})=x^{*}$에서 좌변을 이항하고 정리하면 $f(x^{*}) = 0$을 준다. 이는 우리가 원래 목표로 했던 방정식이다
-. 만약, $x_{n}$이 $F(x_{n})$의 고정점인$F(x^{*})$로 수렴한다면 첫 번재 방정식 $\displaystyle \lim_{x \to x^{*}}x_{n}-c \cdot f(x_{n})$ 따라 $f(x) = 0$또한 도출할 수 있으며,
-. 이제 우리의 목표는 $x^{n}$을 $x^{*}$에 가장 빠르게 수렴시키기 위한 $c$를 찾아내는 것이다.
${(4)}$ 프레임을 바꿔서, $x_{n} - c \cdot f(x_{n})$ 에서 $x^{*}$를 찾는 것을 $x_{n} - x^{*}$을 최소하하는 문제로 변환시킨다면
-. $x_{n+1} - x^{*} = \displaystyle \lim_{x \to x^{*}}(x_{n} - x^{*})-c \cdot f(x_{n} - x^{*})=0$
-. 이 때, $f(x_{n} - x^{*})$는 기울기로 볼 수 있고, 이를 미분의 형식으로 다시 쓰면
$A = \frac{f(x^{*})}{\partial x^{*}}=f'(x^{*})$
-. $x_{n+1} - x^{*} = \displaystyle \lim_{x \to x^{*}}(x_{n} - x^{*})-c \cdot A \cdot (x_{n} - x^{*})=\displaystyle \lim_{x \to x^{*}}(1 - c \cdot A) \cdot (x_{n} - x^{*})$
-. 위 식을 해석하면 $x_{n+1} - x^{*}$ 이라는 '다음 반복의 오차'는 $(x_{n} - x^{*})$ 이라는 '지금 반복의 오차' 에 파라미터 $(1 - c \cdot A)$를 계속 곱하는 것이 된다.
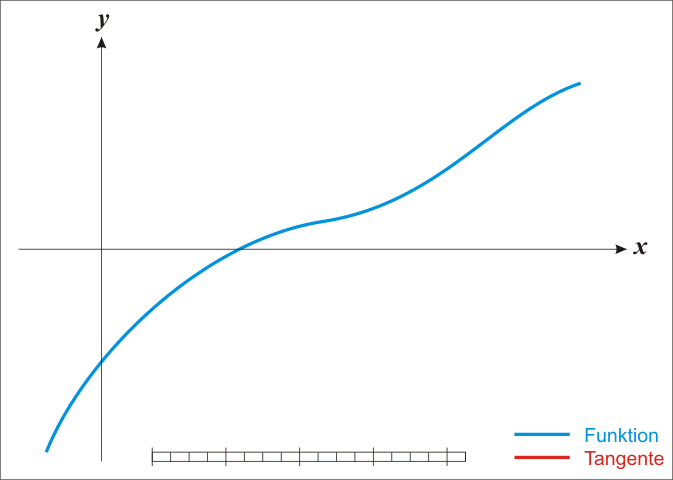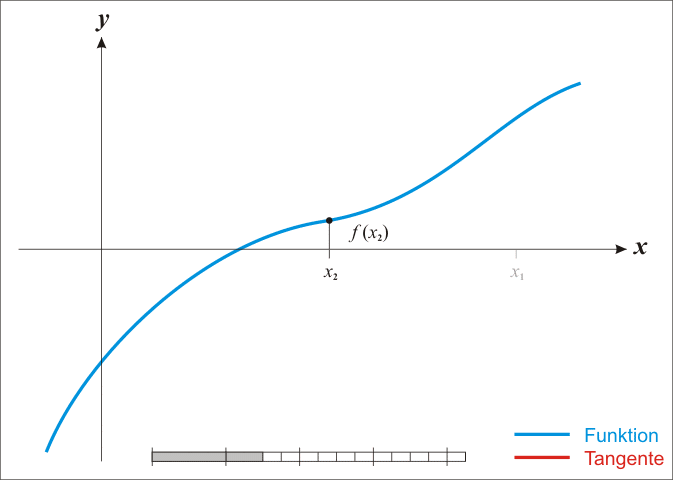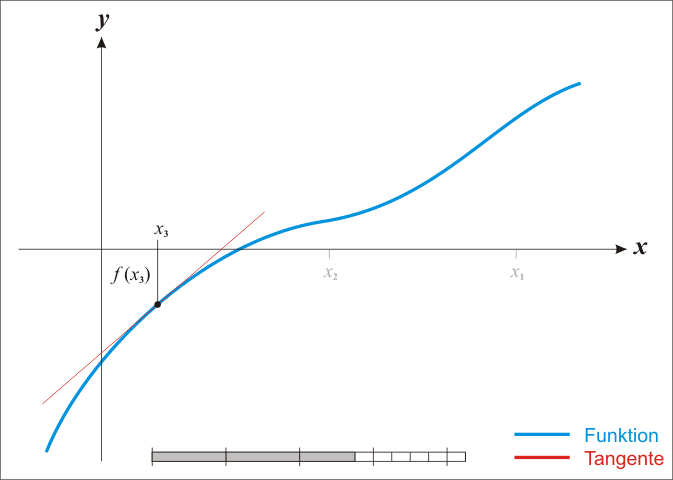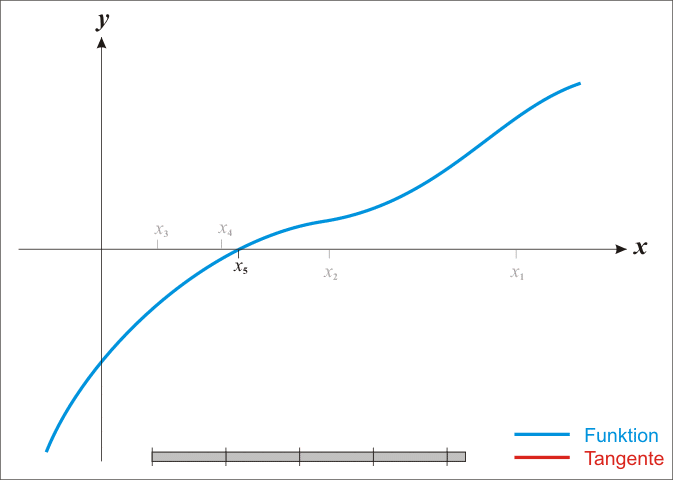
${(5)}$ 이제 거의 다 왔다. $(1 - c \cdot A) < 1$이라면 '다음 반복의 오차'는 '지금 반복의 오차'보다 항상 작게 되며, 어느 순간 우리의 목표였던 $x_{n+1} - x^{*} = 0$을 향에 나아가게 된다.
-. 이 때, $(1 - c \cdot A)$에서 $ c = \frac{1}{A} = \frac{1}{f'(x^{*})}$ 는 $(1- c \cdot A)$를 0으로 만든다=> 가장 최선의 선택이 된다.
-. 물론, 우리는 이 방정식의 해 $x^{*}$을 현재 시점에서 모른다. $x^{*}$은 우리가 처음 있다고 가정한, 우리가 구해야하는 대상이기 때문이다.
-. 따라서, $x^{*}$을 우리가 현재 알수있는 값 $x^{n}$으로 대체하면
$$ x_{n+1} = x_{n} - \frac{1}{f'(x^{n})} \cdot f(x_{n}) = x_{n} - \frac{f(x_{n})}{f'(x^{n})} = 0 $$
이 식이 바로 오차를 0에 최대한 가깝게 만드는 우리가 도출 가능한 최선의 방법론, 즉 뉴턴법이다.
'미적분' 카테고리의 다른 글
| 10. 연쇄 법칙 (0) | 2023.05.17 |
|---|---|
| 9. 평균값 정리와 로피탈의 정리 (0) | 2023.05.15 |
| 7. 최대점과 최소점(정류점) (2) | 2023.05.09 |
| 6. 미분소 (0) | 2023.05.07 |
| 4. 선형 근사 (2) | 2023.05.06 |


