Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
Tags
- bayesian inference
- 프로그래머를 위한 선형대수 #선형대수 #고유분해 #고윳값 #고유벡터
- bayesian
- 미적분 #평균값 정리 #로피탈의 정리 #접선의 방정식
- lightweightmmm
- 미적분 #접선의 방정식 #최적화 #뉴턴법 #뉴턴-랩슨법
- 미적분
- 프로그래머를 위한 선형대수 #선형대수 #LU분해
- Media Mix Modeling
- 수리통계
- 프로그래머를 위한 선형대수 #선형대수 #고유값 #고유벡터 #야코비 회전법 #QR법 #하우스홀더반사 #행렬회전
- 프로그래머를 위한 선형대수 #선형대수 #행렬계산
- 미적분 #사인과 코사인의 도함수
- 프로그래머를 위한 선형대수 #선형대수 #고유값 #고유벡터 #고유분해
- Marketing Mix Modeling
- Optimization
- 시계열분석 #Time-Series Analysis #이상탐지 #Anomaly Detection #Spectral Residual #CNN #SR-CNN
- mmm
Archives
- Today
- Total
문과생 네버랜드의 데이터 창고
7. 최대점과 최소점(정류점) 본문
- 정류점이란?
1) 어떤 함수의 정의역 $x = c$ 근처에서 가장 높은 함수값을 가지는 지점을 국소 최대(극대점), 가장 낮은 함수값을 가지는 지점을 극소점이라고 한다
2) 극대점, 극소점이 전체 함수에서 가장 높거나 가장 낮은 지점이라면, 그 지점을 최대점 혹은 최소점이라고 표현한다
3) 최대점 혹은 최소점은 함수에서 기울기 = 0인 지점(정류점), 미분이 없는 지점(거친점), 정의역의 (양)끝점에서 생성될 수 있으며, 이 때 이 지점들을 임계점이라고 표현한다.
4) 모든 정류점과 거친점, 정의역의 양 끝점에서 f(x)를 구하고, 그 중 최대 / 최소인 지점이 바로 최대점 / 최소점이다 - 정류점과 이계도함수
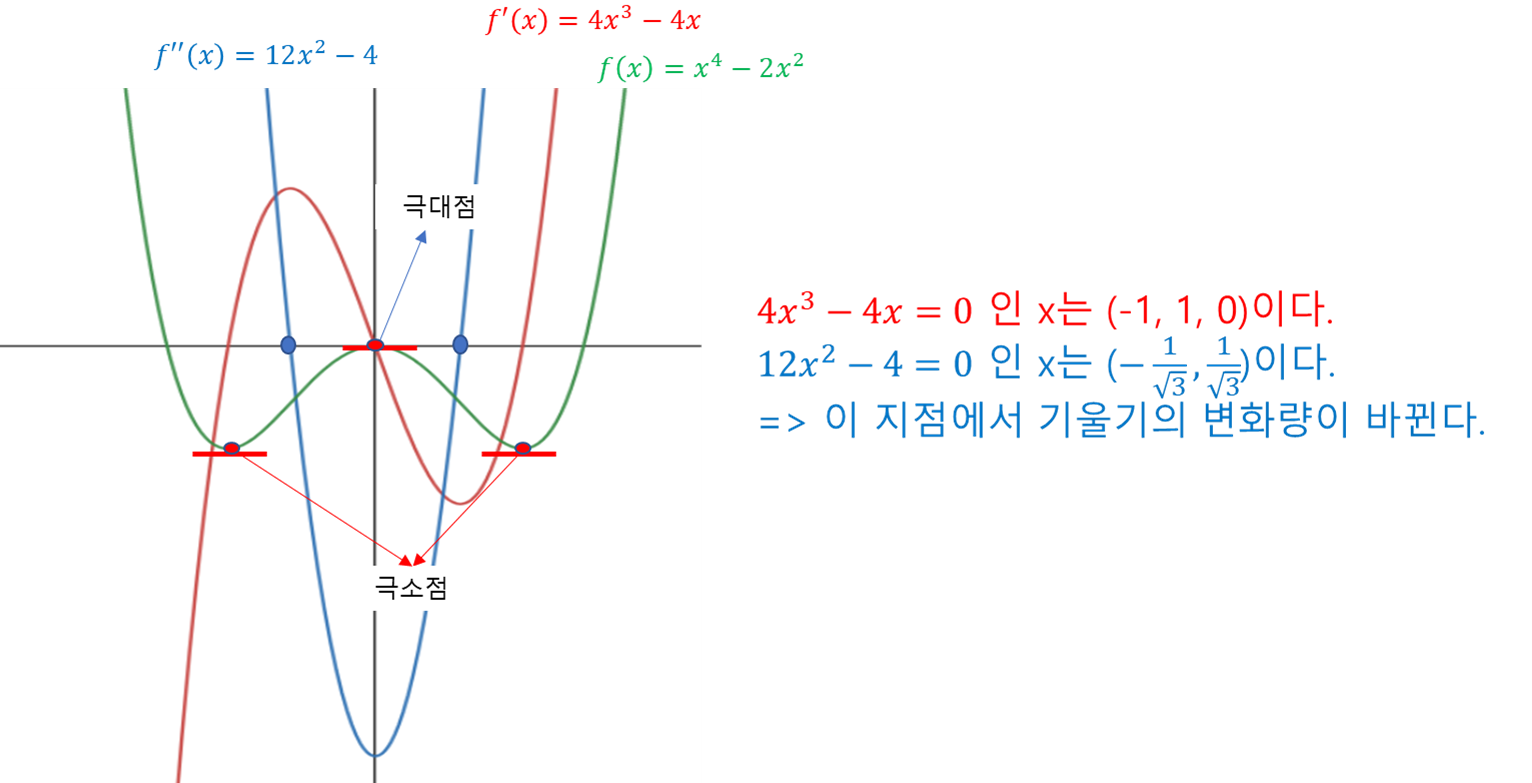
1) $f{(x)}$를 1계 미분한 $f'(x)$는 기울기를 나타낸다
${(1)}$ $f'{(x)}$를 한번 더 미분한 $f''(x)$는 기울기의 기울기를 나타낸다.
${(2)}$ $f(x)$의 입장에서, $f''(x)$는 미분을 두번 한 것이며, 정의에 따라 이는 기울기의 증가(감소)율을 나타낸다.
2) 만약 $f''(x) = 0$인 지점이 존재한다면 그 지점은 기울기의 변화가 0인 지점을 의미하며, 이 지점은 다시말하면 기울기가 증가하거나 감소하기 시작하는 지점(=변곡점)을 의미한다.
2) 극대점과 극소점
${(1)}$ 정의역 $x=c$에서 1계 미분 $f'(x) = 0$인 지점은 정류점이고, $f''(x) > 0$이면 기울기가 증가함(즉, 아래로 볼록)을 나타내므로 이 지점은 극소점이다.
${(2)}$ 정의역 $x=c$에서 1계 미분 $f'(x) = 0$인 지점은 정류점이고, $f''(x) < 0$이면 기울기가 감소함(즉, 위로 오목)을 나타내므로 이 지점은 극대점이다.
'미적분' 카테고리의 다른 글
| 9. 평균값 정리와 로피탈의 정리 (0) | 2023.05.15 |
|---|---|
| 8. 뉴턴법 (0) | 2023.05.13 |
| 6. 미분소 (0) | 2023.05.07 |
| 4. 선형 근사 (2) | 2023.05.06 |
| 3. 미분의 연산법 (0) | 2023.05.04 |


