22. 편미분과 방향미분, 기울기(그레디언트)

1. 편미분이란?
   1) 일변수 함수 $f(x)$가 아니라, 두 개 이상의 변수를 입력으로 받는 함수 $f(x_{1}, ..., x_{n}$이 존재할 떄
   
   ${(1)}$ 이 함수에 대한 미분을 어떻게 구할것인가에 대한 문제가 생긴다.
   
   ${(2)}$ 이 함수에 대하여 오직 한 개의 변수(ex, $x_{1}$의 영향에 대해서만 관심을 갖고 나머지 변수에 대해서는 일단 관심을 끄기로 한다면, 이것을 우린 편미분이라고 부른다.  
   
   ${(3)}$ 엄밀하게 정의한 편미분은 아래와 같이 나타낼 수 있다.

   $\frac{\partial f(x_{1}, x_{2}, ..., x_{n})}{\partial x_{1}} = lim_{x_{1} \rightarrow 0} \frac{\Delta f}{\Delta x} = \frac{f(x_{1} + \Delta x_{1}, x_{2}, ..., x_{n}) - f(x_{1}, x_{2}, ..., x_{n})}{\Delta x_{1}}$

   편미분을 표현할 땐 보통 $\partial$ 기호를 쓰며, 이제 f'같은 라그랑주 표기법은 사용하기 어렵다(어떤 변수로 편미분했는지 알 수 없기 때문이다.) 대신 $f_{x_{1}}$와 같은 표기법을 사용하여 편미분을 표현한다.

   
   ${(4)}$ 위 식을 해석하면 아래와 같다.
   
   -. 어떤 함수가 $x_{1}, ..., x_{n}$을 입력으로 받을 때, 오로지 한 개의 변수(ex, $x_{1}$)의 국소 변화에만 신경쓰고 나머지는 신경쓰지 않겠다는 선언이다
   
   -. $x_{2}, ..., x_{n}$은 요컨데 6,4와 같은 상수로 취급해버리는 것이다.
   
   2) 안장점
   
   ${(1)}$ 각각의 변수들로 편미분한 결과 부호가 서로 다른 경우, 이를 안장(Saddle)이라고 한다.
   
   ${(2)}$ 위와 같은 사례가 정류점 근처(즉, 편미분 값이 0인 지점)에서 발생하는 경우, 이를 특별히 안장점(Saddle Point)이라고 한다.
   
   -. 이 지점은 보는 방향에 따라서 극댓값이거나, 혹은 극솟값이기 때문에 특별하게 취급된다.
   ${(3)}$ 함수에 안장점이 존재하는 경우, 해당 안장점은 정류점(정류점 참조)이지만 이 지점은 극댓값(최댓값)이지도, 극솟값(최솟값)도 아니다.

   정류점에서 극솟값 = 최솟값을 갖는 함수  $f(z) = x^{2} + y^{2}$	정류점에서 극댓값 = 최댓값을 갖는 함수 $f(z) = x^{2} + y^{2} + 2$	정류점에서 안장점을 갖는 함수 $f(z) = x^{2} - y^{2}$ 원점은 정류점이지만 x방향에서 보면 이는 최솟값이며, y방향에서 보면 최댓값이다. 따라서 최솟값인지 최댓값인지 판단이 어렵게 된다.

   
   ${(4)}$ 안장점을 판단하는 방법은 다음과 같다.
   -. 2X2의 경우 : 2차 미분의 행렬, 즉 헤쎄 행렬을 계산하고, 부호가 섞여 있는지 판단한다.

   $\bigtriangledown^{2}(X) = \begin{bmatrix} f_{xx} & f_{xy}\\  f_{xy} & f_{yy} \end{bmatrix}$ 를 계산한 후

   -. $D = f_{xx}f_{yy} - f_{xy}^{2}$ 이 $D>0$인경우 극값이 존재하고, $f_{xx} > 0$이면  $f(f_{x} = 0, f_{y} = 0)$인 지점에서 극솟값을 가진다. -. $D = f_{xx}f_{yy} - f_{xy}^{2}$ 이 $D>0$인경우 극값이 존재하고, $f_{xx} < 0$이면  $f(f_{x} = 0, f_{y} = 0)$인 지점에서 극댓값을 가진다. -. $D = f_{xx}f_{yy} - f_{xy}^{2}$ 이 $D<0$인경우 $f(f_{x} = 0, f_{y} = 0)$인 지점에서 안장점을 가진다.

2. 방향 미분
   1) 일변수 함수와는 달리 다변수 함수는 하나의 지점에서 무한대에 가까운 각도를 가진 방향을 정의할 수 있다.
   
   2) 이 때, 주어진 지점 $P = (x_{1}, ..., x_{n})$에서 구한 기울기 $v = [ f_{x_{1}}, f_{x_{2}}, ... , f_{x_{n}} ]$ 가 있다고 가정하자.
   
   ${(1)}$ 이 때, 방향을 지시하는 어떤 미소한 단위벡터 $u = \begin{bmatrix}  u_{1} \\  ... \\  u_{n} \end{bmatrix}$가 존재하여
   
   -.이 벡터가 가리키는  하나의 방향에 대한 스칼라 기울기 값을 구하는 것을 방향미분이라고 한다.
   ${(2)}$ 위를 엄밀하게 정의하면 아래와 같다.

   ① $D_{u}f(p) = lim_{\Delta s \rightarrow 0} \frac{\Delta f}{\Delta s} = lim_{\Delta s \rightarrow 0}\frac{f(p + u \cdot \Delta s) - f(p)}{\Delta s}$

   ② 이 때, 선형 근사를 사용하여 $\Delta f \approx \frac{\partial f}{\partial x_{1}}\Delta x_{1} + \frac{\partial f}{\partial x_{2}}\Delta x_{2} + .... + \frac{\partial f}{\partial x_{n}}\Delta x_{n}$ 에서 방향 단위벡터 $u = \begin{bmatrix}  u_{1} \\  ... \\  u_{n} \end{bmatrix}$일 때, $\Delta x_{1} = u_{1}\Delta s$, $\Delta x_{2} = u_{2}\Delta s$ ..... $\Delta x_{n} = u_{n}\Delta s$로 표현할 수 있다.

   ③이 때, $\Delta s \rightarrow 0$ 이면, $$D_{u}f(p) = \Delta f = \frac{\partial f}{\partial x_{1}}u_{1} + \frac{\partial f}{\partial x_{2}}u_{2} + ..... + \frac{\partial f}{\partial x_{n}}u_{n}$$ 로 정리할 수 있다.

   ④ 위 식은 벡터 형식으로 $$D_{u}f(p) = \bigtriangledown f \cdot u$$ 로 쓸 수 있으며, 그 값은 스칼라 값으로 도출된다.

3. 기울기(그레디언트)
   1) 방향 미분을 벡터 형식으로 고치면서, f의 모든 변수에 대한 미분값 벡터 $\bigtriangledown f$를 얻었다.
   
   ${(1)}$ 이 때, $\bigtriangledown f$를 기울기 벡터라고 한다.
   
   2) 기울기 벡터는 다음과 같은 특징을 갖는다.
   
   ${(1)}$ 기울기 벡터는 등위 곡선에 수직이다.
   -. $f = 3x + y + 1$인 다변수 함수를 생각하자. 이 때, 이 함수의 방향미분은 $D_{u}f = 3u_{1} + u_{2}$ 이다. 
   
   -. 등위 곡선은 $D_{u}f = 0$인 지점이고 이 때 단위 벡터는 $u = [1, -3]$에 비례한다.
   
   -. 한편, 기울기 벡터는 $\bigtriangledown f = [3,1]$ 이고 , 두 벡터의 내적은 $[3,1] \cdot [1, -3] = 0$ 이다.
   
   -. 이는 등위곡선 $D_{u}f = 0$를 통과하는 벡터와 그 기울기 벡터간 내적이 0이라는 의미이며, 이는 다시 말해 두 벡터가 서로 수직에 위치하고 있음을 알 수 있다.  
   
   ${(2)}$ 기울기 벡터의 방향은 기울기가 가장 가파른 방향이다
   
   -. 기울기 벡터 $\bigtriangledown f$ 와 평행하는(즉, 방향이 일치하는) 단위 방향벡터 u를 상정하자
   
   -. 이 때, 단위 방향벡터 u는 기울기 벡터와 평행하기 때문에 그 벡터는 $\frac{\bigtriangledown f }{||\bigtriangledown f ||}$
   
   -. 이 때, 두 벡터의 내적 $\bigtriangledown f \cdot u = \frac{||\bigtriangledown f||^{2}}{||\bigtriangledown f||} = ||\bigtriangledown f||$의 관계가 성립되고, 이는 해당 함수가 해당 지점에서 가질 수 있는 기울기 중 가장 큰 값이다.(기울기 값의 max는 기울기 자기 자신의 값이다)
   
   -. 따라서, 단위벡터가 기울기 벡터에 평행할 때 기울기 값이 가장 커지므로, 기울기가 가장 가파른 방향은 기울기 벡터의 방향임을 알 수 있다.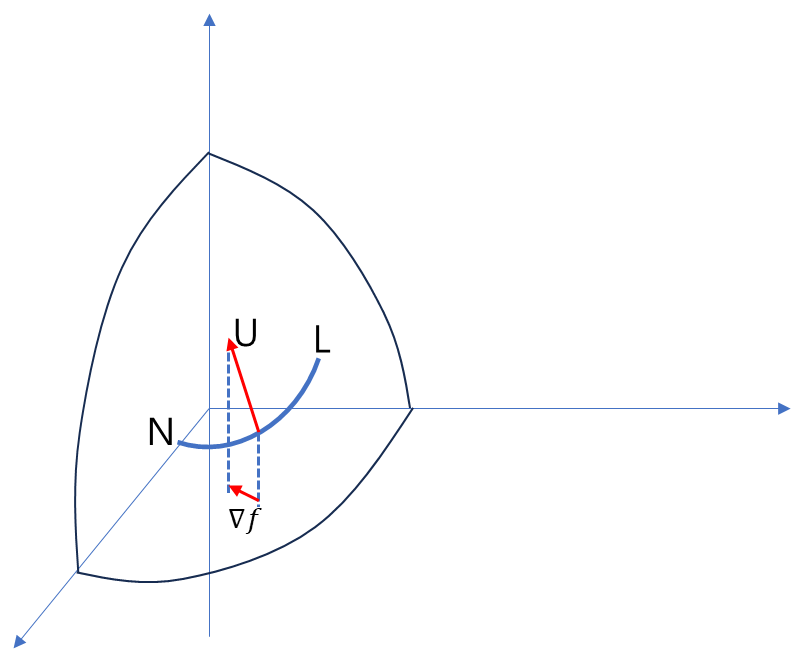

   구의 겉껍질을 타고 가는 등위곡선 NL에서 가장 가파른 방향을 나타내는 벡터 U를 밑면의 2차원 (x,y) 평면에 투영했을 경우, z 성분은 소실되지만 어찌됐든 해당 점에서 가장 가파른 방향을 $\bigtriangledown f$가 가리키게 된다.